Assignment 6: Median of the Road

By Krista Floer

Given line segments j, k, and m. If these are the medians of a triangle, construct the triangle.

To try to understand how to solve this problem, I first drew a triangle and constructed the medians. I found that where the medians intersect is the centroid of the triangle. This can be seen by thinking about how the centroid is constructed. It is constructed by connecting the midpoint of one side of a triangle to the opposite vertex. This is the same way a median is constructed. Thus, we can see how the centroid would be the intersection of the medians.

A property of the centroid is that each median has one-third of its length on one side, and two-thirds of its length on the other side. Using this information, I trisected each median to see where the thirds would lie. This gave me enough information to start with the medians and construct the triangle.

The tool for this is available in a GSP file here. The script view on the tool can be confusing, so I stated the steps here. I also added in a little commentary and some pictures if you do not have/want to use the GSP file.

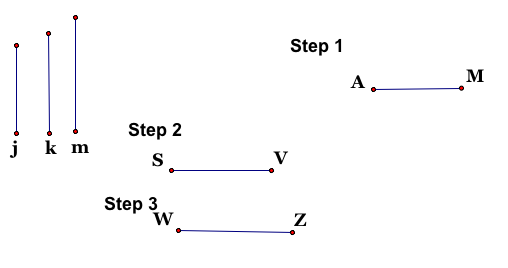
Step 1: Construct a line segment with the same length as j. Label the endpoints A and M. You don't have to use j first. Any segment can be used first, you just have to keep straight which ones you have already used later in the construction.

Step 2: Construct a line segment with the same length as k. Label the endpoints S and V.

Step 3: Construct a line segment with the same length as m. Label the endpoints W and Z.

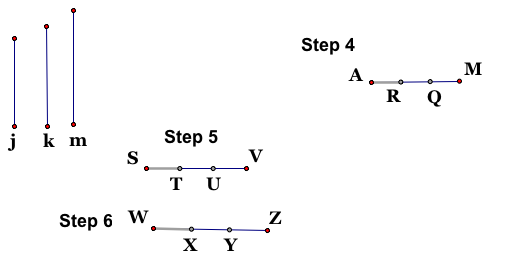
Step 4: Trisect segment AM. Label the points R and Q so that AR = RQ = QM. This will be in the actual construction of the triangle.

Step 5: Trisect segment SV. Label the points T and U so that ST = TU = UV. This will be used to construct the triangle, but this segment will not be in the construction.

Step 6: Trisect segment WZ. Label the points X and Y so that WX = XY = YZ. This will be used to construct the triangle, but this segment will not be in the construction.

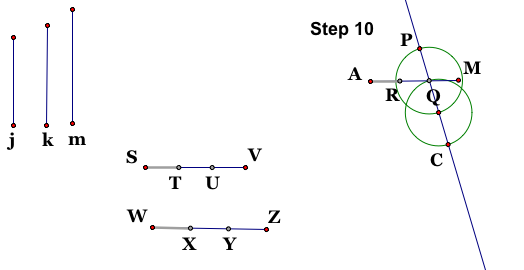
Step 7: Select point Q as your center and use ST as your radius to construct a circle.

Step 8: Select point R as your center and use WX as your radius to construct a circle.

Step 9: Pick either point that the two circles intersect. Either one will be fine. Label this point P. I usually pick the top intersection point.

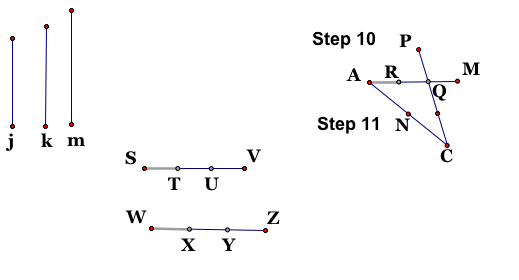
Step 10: Construct a line through point P and Q. Using Q as the center and P as the radius, construct a circle. Using the point where the circle intersects the line opposite of p, mark this as your center and Q as the radius. The new point is the one you want. Label this point C. Hide everything we just used so that you can see segment CP. This is the median m.

Step 11: Connect points A and C in a segment and construct the midpoint. Label this point N.

 

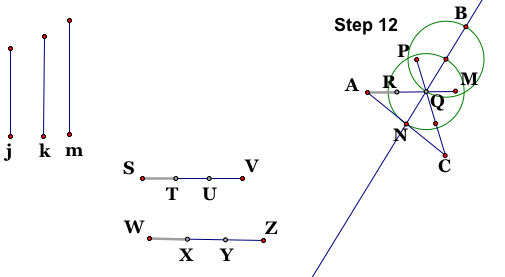
Step 12: Construct a line going through N and P. The length NP is one-third of median k. Going through the same process in 11, we find point B. Connecting B and N, we now have median k.

Step 13: Construct AB and BC. We now have constructed the triangle ABC given the medians j, k, and m. I hid all of the construction lines so all you can see are the medians and the side of the triangle.

Go Back to HOME